Discover what is artificial intelligence models: are not intuitive if you don’t have a minimum knowledge of the discipline. They seem like a black box that can do anything, but at CHECKTOBUILD we know that it has its limits. In this blog we will seek to clarify the main keys to how these models work.
Let’s start by identifying the most common words: Artificial Intelligence, Machine Learning and Deep Learning. These are the most popular words in innovation meetings, but they have a rather fuzzy definition. Let’s delimit their scope.
What is artificial intelligence?
What is artifical intelligence? Any system capable of solving a problem based on its own knowledge, whether manually injected or autonomously learned, is called artificial intelligence. Yes, in these terms almost anything can be called artificial intelligence. The scope is very diffuse. In this field we find for example rule-based systems, first-order logic, decision trees, etc.
Machine Learning, however, is already tighter. It is a subset of AI techniques that autonomously learn to solve a problem. This is different from other AI techniques in that you cannot encode knowledge manually, using rules or heuristics for example. For them to learn they need “solved exercises” in massive quantities.
That is, large records of historical input data and their expected answer, the solution that would be given to the problem. This area includes everything from traditional statistical linear regressions (but adapted for learning) to artificial neural networks.
Finally we have Deep Learning. This is a subset of Machine Learning techniques that are based solely on artificial neural networks. In the following image we can see this hierarchy graphically.
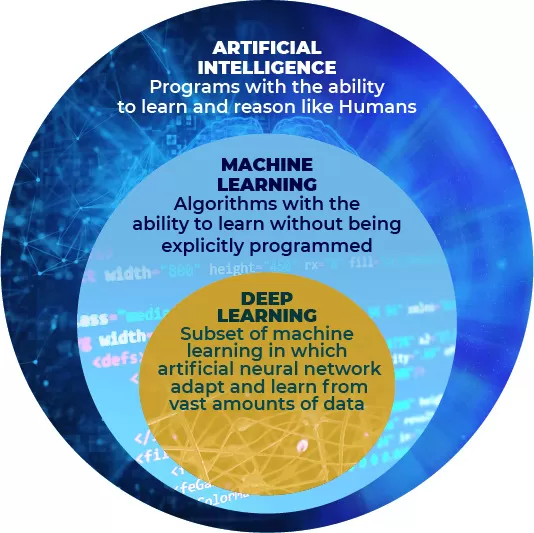
At this point I would like to focus on models that are purely defined within the Machine Learning umbrella. That is, models that learn, and really learn.
What does the Machine Learning model learn to solve?
A Machine Learning model learns to solve a particular and strictly well-defined problem through those expected answers we mentioned at the beginning. We can prepare it to learn a richer and more complex answer to the problem, but it is still empirical behaviour, it will not give answers it has never seen before, it has no imagination. But this is still a very fuzzy and high-level definition.
What exactly does it learn?
What the AI model actually learns is a mathematical equation that relates the input variables (our X) and the expected response (our Y). In other words, if our problem is extrapolable to a function Y=f(X), our Machine Learning model learns the f.
To do so, it must find out how the input variables are related (if they multiply, add, etc.) and the weight of each of them in the problem. In other words, it must find out the coefficients that multiply each term of the equation.
Let’s see a simplified example, my problem to solve is to determine the estimated price of a new car based on its characteristics (X1 = height, X2 = width, X3 = length, X4 = boot volume, X5 = cylinder capacity). The model must learn the mathematical function that relates Xs (characteristics) to Y(price). Let’s assume that this is the final function it has to find out:
f(X1, X2, X3, X4, X5)=8.2*X1 -2.1*X2 +16.5*X3 +0.01*X4 +4.1*X5 +5370
An important note, this function above is very similar to a normal statistical regression, or in other words, a single-neuron artificial neural network.
Of course this is an example explained in summary form, but it involves the fundamental concepts to understand what is going on inside an artificial intelligence model.
As anticipated, in order to learn, our model has to learn from a large number of examples made up of input variables and their expected response. Typically, this will involve handling one or several excels whose columns are these variables (X1, X2, X3, X4, X5, Y) so that their rows give us information such as the following:
f(150, 180, 440, 450, 1500) = 19,636,5 €
How does the Machine Learning model learn to solve the problem?
Let’s recap what we have, a function that we don’t know but that defines our problem and an excel with a bunch of examples, of “exercise results” that will help the Machine Learning model to learn empirically from the data and extract their relationships.
There are algorithms that define the procedure of how to go through the data and use it to find out the objective function (the value of its coefficients). The most famous of these procedures is the Stochastic Gradient Descent (SGD) algorithm and could be summarised in the following strategy.
First we start with a random function, which relates the input variables randomly. We then run through the data, applying the function to that input and calculating the error it makes. There are many methods for calculating this error, but they all essentially do the same thing, compare the response of the function with the expected response we have beforehand.
With that error captured, the coefficients are updated to a greater or lesser extent depending on how large or small the error is in each data run. In this way, with the first learning data, large errors will be made and consequently large corrections to the coefficients. As more and more data is seen, the coefficients associated with each variable will approach the optimum and the system will begin to fail less, it will have found the function that solves the problem.
This is a very conceptual interpretation of the problem that leaves a lot out. However, it achieves the objective we were looking for at the beginning of this post, to provide an insight into the enigma behind artificial intelligence models, so that they do not seem like magic or science fiction. In addition, we have been able to differentiate between AI and Machine Learning, as well as to clarify what problems they aim to solve and the internal mechanisms that support learning.
We cannot talk about artificial intelligence without mentioning new tools. Find out what is ChatGPT and artifical Intelligence.

